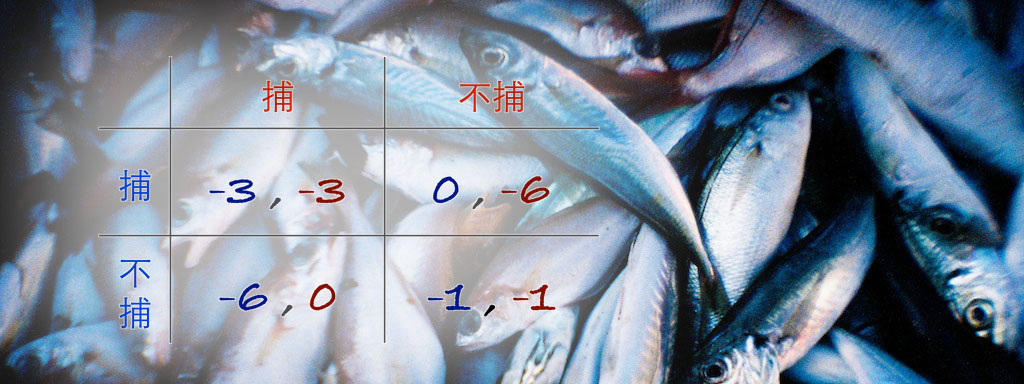
報償矩陣
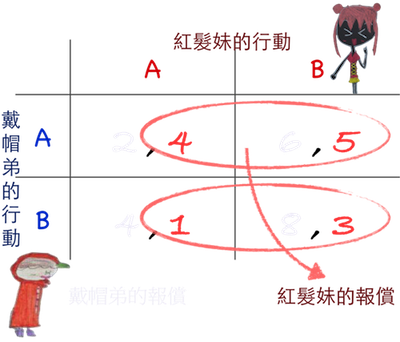
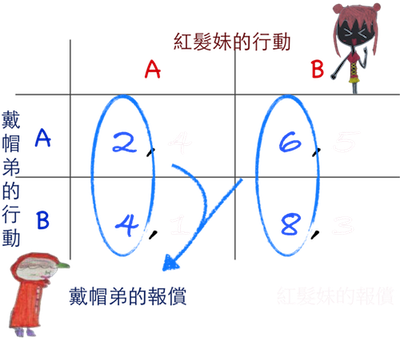
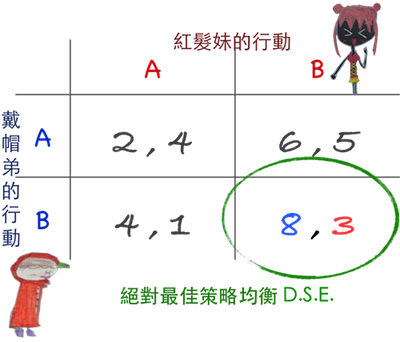
從紅髮妹來看:
當戴帽弟選取A時,
因為第一列自己的報償 4<5,故選擇B。
當戴帽弟選取B時,
因為第二列自己的報償 1<3,故選擇B。
因此紅髮妹有絕對最佳策略B。
從戴帽弟來看:
當紅髮妹選取A時,
因為第一行自己的報償 2<4,故選擇B。
當紅髮妹選取B時,
因為第二行自己的報償 6<8,仍應選B。
所以戴帽弟也有絕對最佳策略B。
Nash 均衡
每位Player在對手特定行動下,做出自己最有力的行動,所共同達成之狀態。
同時賽局(Simultaneous)
Player同時作決策,實際上並沒有先後行動的差別。
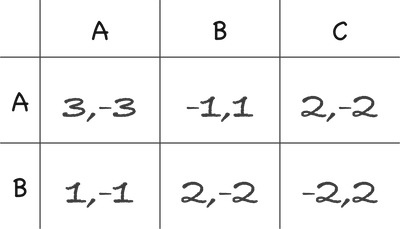
Ex.1
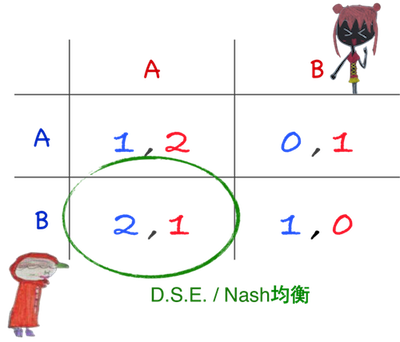
從紅髮妹角度
戴帽弟如果選A,其應選A,
戴帽弟若選B,其仍應選A,
表示有絕對最佳策略A。
同理戴帽弟也有絕對最佳策略B,
因此 DS 均衡是左下位置。
Ex.2
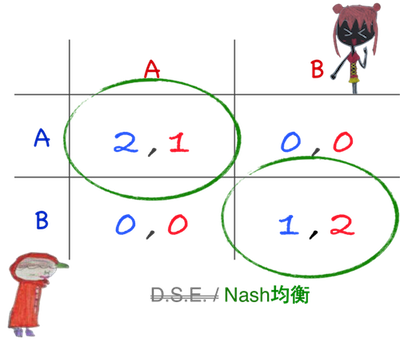
從紅髮妹角度,
戴帽弟如選A,其應選A,戴帽弟若選B,其則應選B,
此時無絕對最佳策略!
同理戴帽弟角度:
紅髮妹如選A,其應選A,紅髮妹若選B,其則應選B,
此時亦無絕對最佳策略!
此時無DS均衡是肯定的,但Nash均衡呢?
此時若戴帽弟和紅髮妹皆選A,則就是一個Nash均衡。
同時若戴帽弟和紅髮妹均選B,也是另一個Nash均衡。
若我們直接看左上角 (2,1),
由於戴帽弟在紅髮妹選取A時,
選擇A確實是自己的最佳行動,故無動機改變。
同理紅髮妹在戴帽弟已選A時,
選擇了A也已是最佳,故兩人皆無動機改變。
先後行動(Sequential)
領導者(Leader)先行動,追隨者(Follower)後行動。
Ex.1
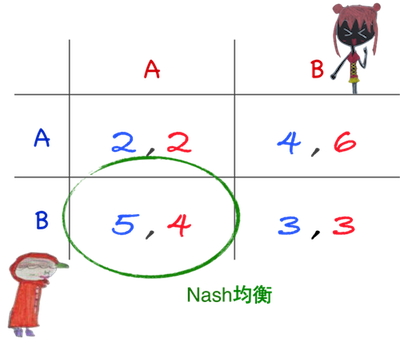
如果戴帽弟先行動,紅髮妹後行動,均衡會在哪呢?
依照逆推擴展邏輯(Backpropagation),
可把狀況畫成賽局樹(Game Tree)來沙盤推演,
而兩人各自最後會得到的報償列在後端。
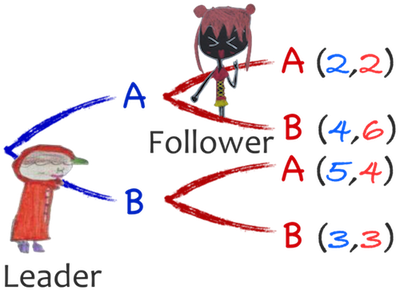
戴帽弟如果選了A,
後行動的紅髮妹也有兩種選擇,
此時紅髮妹一定會挑選B,因為 2<6;
而若戴帽弟選擇B,此時紅髮妹必選A。
對戴帽弟而言,
等於只要從4與5之中作選擇即可。
因此答案很明顯:
蜘蜘應該選B,而只要紅髮妹理性,她必選B。
特別注意:
上述邏輯背後有一強列的假設:
先行動者握有對方報償矩陣數字資訊!
因此先行動者是握有發牌權的,
而後行動者相對只能被動的看著辦。
⌘ 統計學中也有類似賽局樹的工具,稱為「決策樹」
生活中也有類似的東西,那就是「族譜(Family Tree)」